Diferenciální rovnice k Vánocům

Mohli bychom jí říkat Vánoční rovnice (Marry Christmas Equation) a nikdo zatím neví, kdo s ní přišel jako první. Něco jí však celé ty roky chybělo – šlo pouze o transcendentní rovnici s 6 proměnnými. Není nic snazšího než spojit x a y do funkce, ostatní písmenka považovat za parametry a celou věc povýšit na diferenciální zderivováním y podle x.

Původní rovnice

Bing AI vám sice bude tvrdit, že rovnice byla zpopularizována někdy do roku 2018, na YouTube můžete najít videa s řešením už od roku 2013, avšak přes Google dokážeme zachytit i odkazy na eshopy s tričky, na kterých je vyřešená už v roce 2003. Zapíšeme ji úplně jako:

$y=\dfrac{\ln{\left(\dfrac{x}{m}-sa\right)}}{r^2},\qquad r,m\neq0,\,\dfrac{x}{m}>sa\,.$

Cílem řešitele je dostat rovnici do tvaru:

$me^{rry}=x-mas\,,$

což není obtížné, uvědomíme-li si význam přirozeného logaritmu a pak přeuspořádáme ostatní písmena, jako by byly dalšími proměnnými.

Diferenciální rovnice

Adresátovi můžeme cestu k přáníčku trochu prodloužit, a to předpokladem, že sama původní rovnice ve tvaru $y=\dots$ je vlastně řešením diferenciální rovnice a že proměnná $y$ je ve skutečnosti závislá ve funkci $y(x)$ . Zderivováním $y$ podle $x$ dostaneme cosi, co bude při zpětné integraci dobře dávat původní Vánoční rovnici. Většinu odvození přenechám čtenáři, abych jej neobral o veškeré kouzlo svátků. Takzvaná Marry Christmas Differential Equation může být zapsána:

$y'=\dfrac{1}{r^2\left(x-mas\right)}\,,$

kde definiční obor musí být trochu striktnější:

$m\in\mathbb{R}^{+},\qquad r\in\mathbb{R}\setminus 0,\qquad x,a,s\in\mathbb{R} : x > mas\,.$

Po integraci by dořešení bylo trochu otravné nebýt „počáteční“ podmínky:

$y\left(m(as+1)\right)=0\,.$

Pamatujme, že z integrační konstanty můžeme jako králíky z klobouku vytahovat cokoli je zrovna potřeba. Bezradnému příjemci našeho přání také můžeme poradit, že by určitě ve výsledném přání nemělo chybět písmeno „ $e$ “, avšak explicitní řešení ODR (nyní mezikrok) můžeme utajit. Cesta až od ODR k „merry xmas“ tak může být delší a zajímavější.

Pro zájemce, zde je PNG zadání, které si můžete libovolně přeuspořádat a adaptovat pro svá přáníčka.

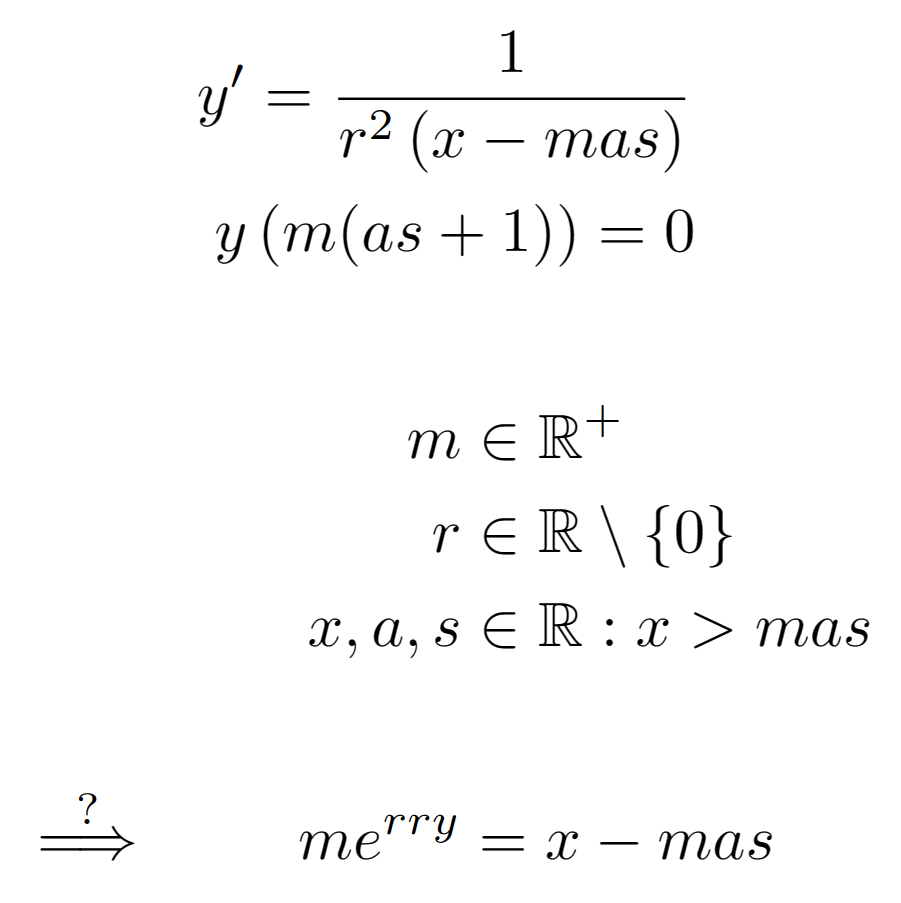
Na závěr bych vyzval všechny matematiky k dalšímu ztěžování úlohy a rozvoji do dalších řádů a typů rovnic. Můžete svá řešení odkázat třeba i sem do komentářů. 😉